11 Best High-Speed PCB Routing Practices

[rahuls]

Originally published at: https://www.protoexpress.com/blog/best-high-speed-pcb-routing-practices/

A PCB designer has a difficult task when it comes to routing a circuit board. Things get a lot more complicated when the design involves high-speed signals. In an effort to help these PCB designers, we have drafted a list of best high-speed PCB routing practices that will assist them in achieving that perfect high-speed design.

[Rachel]

I’m currently working on a high-speed PCB design and have some questions about transmission line effects. From my understanding, when we talk about “transmission line” effects, we refer to issues like crosstalk, reflections, and ringing. These effects don’t usually appear at low frequencies where the PCB trace behaves more like an ideal transmission medium, similar to how we expect a wire to behave based on early school lessons.

I also understand that the 50-ohm value isn’t related to the line resistance, which is typically very small and less than 1 ohm. Instead, this value comes from the ratio of the inductance (L) and capacitance (C) on the line. Adjusting the trace height above the ground plane (affecting C) or changing the trace width (affecting L) can change the impedance of the line.

Since the reactance of L and C depends on the signal frequency, I have a few questions:

1. Why don’t we refer to this as “line reactance” instead of “line impedance”?
2. How can it be just 50 ohms? Shouldn’t it be dependent on the signal frequency, like 50 ohms at 1 MHz?
3. What happens if I choose a 100-ohm or 25-ohm trace instead? I know we like to think of 50 ohms as a standard value, but it’s never exactly 50.0000 ohms.
4. Is there any situation where the actual resistance of a PCB trace might matter?

[BerndKruger]

First, let’s have a look at the formula and equivalent circuit for a transmission line:

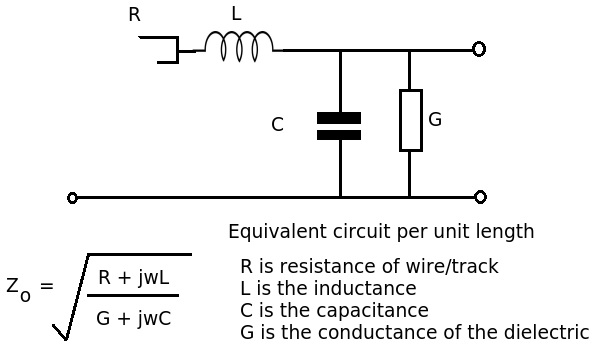
1. Impedance vs. Reactance

Reactance describes the opposition to changes in current or voltage for individual components like inductors and capacitors. A transmission line, however, incorporates resistance (R), inductance (L), and capacitance (C), making impedance the appropriate term. Impedance is defined as the ratio of the voltage phasor to the current phasor in a transmission line, encompassing all these elements.

2. Why 50Ω?

The 50Ω impedance arises from the ratio of inductance to capacitance per unit length of the transmission line. When R is much less than jωL and G is close to zero, these values become negligible, simplifying the expression to the square root of L/C, making it frequency-independent.

3. Deviating from Standard Impedance

Technically, you can choose any impedance, such as 100Ω or 167Ω, but it’s generally advisable to stick to standard values like 50Ω. This is because finding compatible components, such as connectors for non-standard impedances, can be challenging. Additionally, there are extensive resources and guidelines available for designing transmission lines on PCBs. As a side note, the impedance of free space is 376.73031… ohms, which is an interesting fundamental constant of our universe.

4. When Actual Resistance Matters

At low frequencies, the resistance (R) of the transmission line may become significant as the inductive reactance (jωL) is small. At very high frequencies, dielectric losses can also become a concern, affecting the performance of the transmission line.

[myrtlee]

A transmission line inherently possesses distributed inductance and capacitance throughout its length, which can be conceptualized as countless small inductors and capacitors arrayed along the line, as shown below:

Each inductor slows down the rate at which its corresponding capacitor can charge. As we continue to subdivide the transmission line into smaller and smaller segments, the inductors and capacitors become proportionately smaller as well. But does this subdivision affect the line’s behavior? Not really. We can slice the transmission line into any number of segments—from just a few to an infinite number—making the inductors and capacitors arbitrarily small in the process.

The critical insight here is that the absolute values of these inductors and capacitors are not what dictate the line’s properties. What truly matters is the ratio of inductance to capacitance, a value that remains constant regardless of how much we divide the line. Since the characteristic impedance of the transmission line is determined by this ratio, it remains unchanged whether the line is divided into more segments or made longer. This consistency is key to understanding why the fundamental behavior of the transmission line doesn’t shift as we alter its segmentation or length.

[Lieniner]

Building on what Myrtle mentioned:

Consider a long chain of inductors and capacitors, all starting with 0 Volts and Amps. When you introduce a voltage step at one end, the inductors slow down the charging of the capacitors, causing a steady current to flow. This current is proportional to the voltage you applied. By dividing the voltage by the current, you can determine the resistance that this infinite transmission line mimics. In an ideal infinite transmission line, it behaves just like a resistor from the outside.

However, this behavior only holds if the voltage step can continue to propagate down the line. Here’s the key insight: if you have a short transmission line but add a resistor matching the characteristic impedance across its end, the line will appear infinite from the perspective of the source. This technique is known as terminating the transmission line.

[will]

Bernd has provided an excellent overview. I’d like to expand on a couple of points:

2) The 50 Ohms Impedance: While 50 Ohms is considered a standard value, it’s worth noting that the dielectric constant of the material does exhibit slight frequency dependence. This means that the impedance you calculate for a trace at 1 GHz will differ slightly at 10 GHz. However, this variation is usually small and only becomes a concern in very high-frequency designs. If you’re working one high-speed PCB design, you’re likely already aware of the nuances involved.

4) Impact of Resistance on PCB Traces: For typical PCB designs using FR4, dielectric losses start to become significant around 0.5 to 1 GHz. However, resistance is a critical factor when dealing with high-current lines. For instance, a 6 mil wide trace of 1 oz copper carrying 1 Amp over a 1-inch length will have approximately 0.1 Ohms of resistance. This translates to a 0.1V voltage drop and a temperature rise of around 60°C. If such a voltage drop is unacceptable for your design, you’ll need to either widen the trace or use thicker copper.

As a general guideline, if your trace lengths are under 1 inch, DC resistances can often be considered negligible.

[Sophia]

The reason why the effective impedance of an ideal transmission line remains constant can be explained in a straightforward way. When we refer to a “transmission line,” we’re talking about wires that are considered “long” relative to the wavelength of the electromagnetic wave traveling through them. “Long” here means that the physical length of the line is greater than the wavelength of the signal being transmitted. This concept becomes particularly significant at high frequencies or over long distances. The relationship between the wavelength of a signal and the length of a trace is crucial.

As has been noted, every trace on a PCB has a certain inductance and capacitance per unit length. These values are typically expressed as L (inductance per unit length) and C (capacitance per unit length). The total inductance and capacitance of a segment of the transmission line would then be the product of these per-unit values and the segment’s length (i.e., L_total = L * length and C_total = C * length).

Now, think about a sine wave traveling along this transmission line. In the context of a dielectric or air medium, electromagnetic waves propagate at nearly the speed of light (around 150 ps per inch). At any given moment, a specific portion of the sine wave interacts with a segment of the trace equivalent to its wavelength. Lower frequency waves have longer wavelengths, meaning they interact with a longer segment of the trace, thus encountering greater inductance and capacitance. Conversely, higher frequency waves have shorter wavelengths and interact with shorter segments of the trace, encountering lesser inductance and capacitance.

The key point here is that both the effective inductance (L) and capacitance (C) that a wave “sees” are proportional to the wavelength of the signal. Since the characteristic impedance of a transmission line is given by Z0=√(L∕C), the proportional relationship between L and C with respect to wavelength cancels out. As a result, waves of different frequencies perceive the same effective impedance Z0.